Bloom Filter

2021-04-07 约 1317 字预计阅读 3 分钟

次阅读

摘要

该算法以hash函数为基础，主要用来解决membership问题，也就是判断某个元素在不在某个集合中，可以在常数时间进行判断，但是判断结果可能存在假阳性的问题，也就是一个元素不在集合中，但是却被误判为在。该算法的实现同样是采用了以减少精确度换取较小的空间开销的思想，具体损失多少精度，又能换回多少空间是本文要解决的问题。

算法

该算法很简单且优美，下面对其进行简单描述，首先初始化一个长度为$m$的比特串$B$，并选择$k$个$[N]\to [m]$的hash函数，对于一个每一个元素都属于$[N]$的长度为$n$的集合$S$，对其进行如下操作：

Set B[.]=0
for i=1 to n do
- for j=1 to k do
  - $B[h_j(S_i)]=1$

算法很简单，就是对每一个元素，用所有的hash函数进行计算，并将所计算出的所有位置置1。查找也很简单，就是进行类似的操作，如果元素$q$的所有的hash值对应的值均为1，那么就判断元素在该集合中。显而易见，如果$q$真的在集合中，那么肯定能得到肯定的结果，但是得到肯定的结果不代表其一定位于集合中。因为会存在假阳性的问题，所以现在的问题就是如何评估假阳性出现的概率，以及如何选取$k$和$m$的值来使内存占用和准确度都能比较好呢？

分析

首先分析对于一个元素，其不在集合当中，但是将其判断为在集合当中的概率。假设该元素经过hash函数计算之后的值分别为$a_1, a_2, …, a_k$，对于任意一个$a_i$的值为0的概率为： $$ P(B[a_i]=0) = (1-1/m)^{nk} $$ 因为假设所有的元素的hash值服从均匀分布，所以落到每一点是等概率的$1/m$，而只有当所有元素的所有hash值（共$nk$个）都没落到$a_i$点，其值才为$0$。

然后计算一个元素假阳性的概率，其假阳性代表所有的hash值对应的点均为$1$，即： $$ P(\forall.i\ B[a_i]=1) = (1-(1-1/m)^{nk})^k $$ 然后又根据当$m$的值较大时的近似公式： $$ (1-1/m)^{nk}=e^{-nk/m} $$ 可以将上述公式化简为$(1-e^{-nk/m})^k$。我们希望该值尽可能的小，因此在$m,n$值确定的情况下，我们希望通过$k$值的选取使得其值尽可能的小，求$(1-e^{-nk/m})^k$的最小值就相当于求$k\cdot ln(1-e^{-nk/m})$的最小值。求导应该可以算出来，但这里有一个技巧，我们假设$p=e^{-nk/m}$，则上式可以化为： $$-\frac{m}{n} \ln p\ln(1-p)$$ 根据对称性，可知当$p$取$1/2$时，其值最小,此时k的值为$\frac{m}{n} \ln2$。该网站有一个相应的对应表格，我们截取一部分如下图所示：

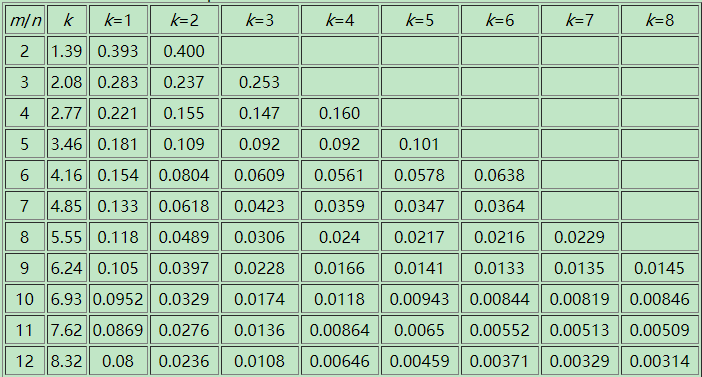
从图中可以看出，当$m/n$比例一定时，假阳性的值随$k$先减小再增大，比如当$m/n=9$时，其最小值在$k=6$处取得。

我们已经算出了$k$的最优取值，将其代入到假阳性计算公式中可得： $$ P = (1/2)^{\frac{m}{n} \ln2} \approx (0.6185)^{m/n} $$ （居然是黄金比例0.618😮）

如果我们想让其错误率小于$\epsilon$，就需要计算 $$ (1/2)^{\frac{m}{n} \ln2} < \epsilon $$ 通过上式可得，$m$的取值范围为$m > n\log e \log\frac{1}{\epsilon} \approx 1.44 n \log\frac{1}{\epsilon}$。所以该方法总的空间复杂度为$k$个hash函数和一个比特串的开销，即： $$ k \log n + n \log(1/\epsilon) = (n + \log n) \log(1/\epsilon) $$ 感觉占用的空间也不小啊~

以上就完成了大概的分析，但其实专业的分析好像很复杂，我尝试了一下，没看懂😂

实现

TODO

目录

Bloom Filter

摘要

算法

分析

实现

参考文献